堆树详解及使用最大堆实现优先队列
定义
堆树的定义如下:
堆树是一颗完全二叉树;
堆树中某个节点的值总是不大于或不小于其孩子节点的值;
堆树中每个节点的子树都是堆树。
当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。
构造二叉堆
这里是一自定义的动态数组作为底层来实现最大堆这种数据结构,使用数组存储二叉堆具有如下性质,如下如所示:
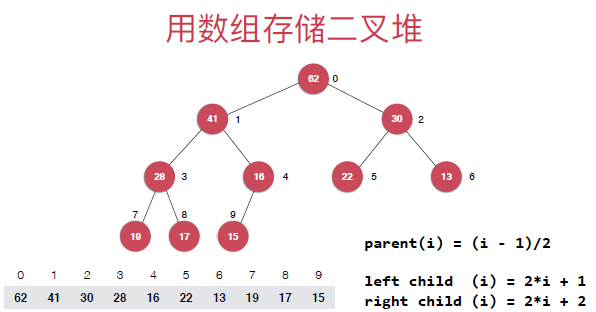
就是通过其中的任何一个节点可以找到其父节点或者是左孩子和右孩子节点。
1 | public class MaxHeap<E extends Comparable<E>> { |
关于判断堆的大小及是否为空都是很简单的操作。就不在这里多说了。下面说一下最大堆中的sift up,sift down和heapify操作。
向堆中添加元素及sift up
对于下面的一个堆,插入元素52时,因为我们使用的是数组存储的二叉堆,然后插入的元素需要满足二叉堆的性质,如果直接通过遍历数组来找到其位置,复杂度是O(n)的,这里采用的是sift up也就是先将元素插入堆的末尾,然后通过上浮操作来找到其位置,复杂度是O(logn)的。
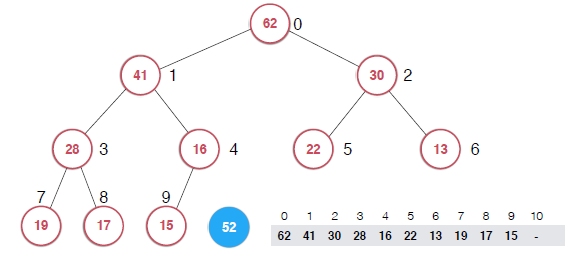
sift up具体实现如下图:
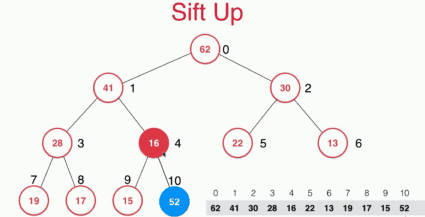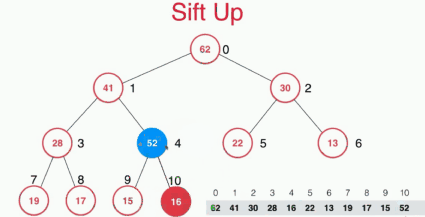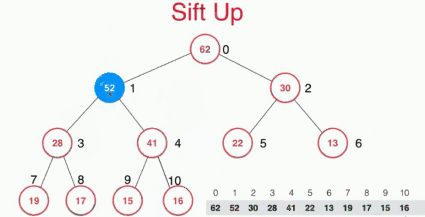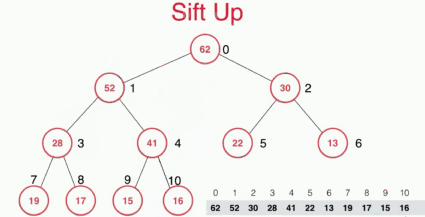
具体的实现如下:
1 | ** |
取出堆中最大元素及sift down
通过性质我们可以知道对于一个最大堆来说,堆中最大的元素在堆顶。取出堆顶的元素之后谁去堆顶?这里采取的操作时将堆顶的62元素和堆底的16交换然后删除16,再将16下沉,找到其合适的位置。这样的复杂度只有O(logn).
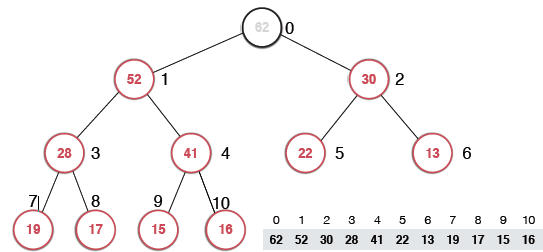
sift down 具体的实现如下:
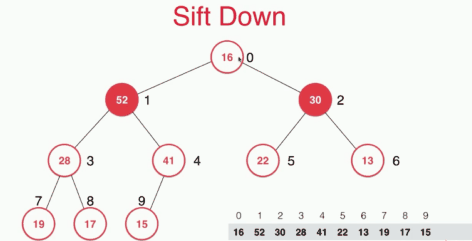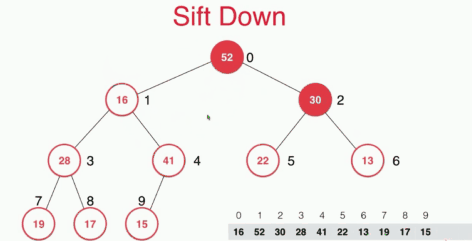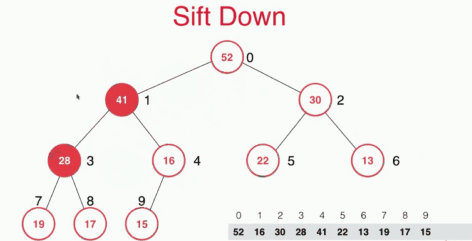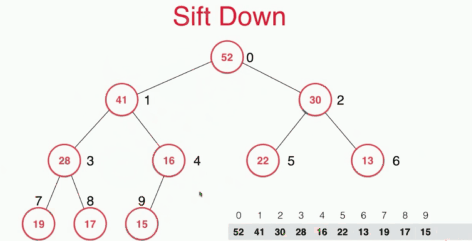
具体代码如下:
1 | /** |
将任意数组整理成最大堆和heapify
一般随便一个数组是不符合最大堆的性质的,如何将一个数组整理成最大堆呢?寻常的想法是将数组中的n个元素不断的插入空堆中,这样操作的复杂度是O(nlogn)的,这里采用heapify的操作来实现,其实就是将不是叶子结点的元素全部采用下沉操作,找到自己的位置,时间复杂度为O(n)的。
heapify的操作具体如下:
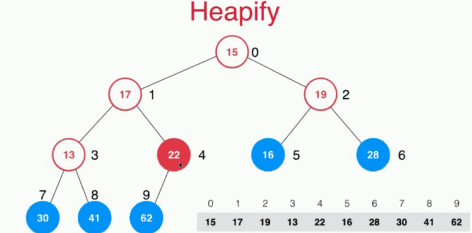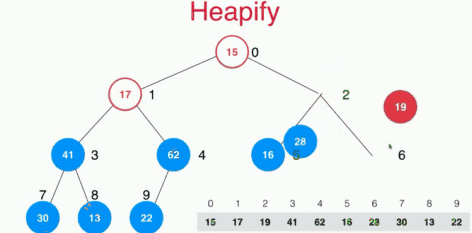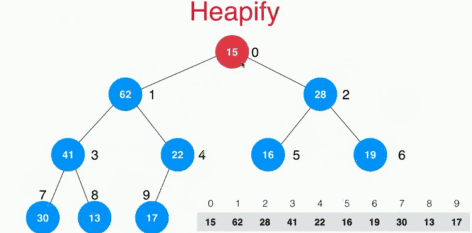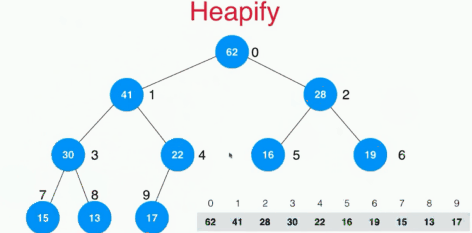
具体的代码实现如下:
首先是数组的初始化
1 | public Array(E[] arr){ |
然后是最大堆中的实现:
1 | /** |
替换堆中的任意元素
是实现的方法比较简单,就是将堆中的最大元素由替换元素替换,然后进行下沉操作,O(logn)的时间复杂度
1 | /** |
完整代码
1 | package heap; |
作为底层的数组的实现如下:
1 | package arrary; |
基于最大堆实现优先队列
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。优先队列有很多的实现方式,但通常采用堆数据结构来实现。因为这两者很像。
具体的实现如下:
1 | package heap; |
应用统计前k个出现频次高的数字
Given a non-empty array of integers, return the k most frequent elements.
Example 1:
1 | Input: nums = [1,1,1,2,2,3], k = 2 |
Example 2:
1 | Input: nums = [1], k = 1 |
Note:
- You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
- Your algorithm’s time complexity must be better than O(n log n), where n is the array’s size
使用优先队列来解决这么问题比较方便,将前k个频次最高的元素放入队列,优先级高的元素出现的频次是这k个中最小的,然后只要有出现频次比他高的就可以替换掉。
1 | package heap; |
然后觉得太复杂了,然后又改了改,就是存入hashmap之后,因为其出现的频次对应的是value的值,然后让hashmap根据value排序,然后输出即可。
hashmap根据value排序需要先将其视图存入list中,然后使用collections的排序方法来做,实现一个Comparator的比较器就可以了,代码化简不少。
1 | package heap; |
