并查集详解及底层实现

定义

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

并查集（Union/Find）从名字可以看出，主要涉及两种基本操作:合并和查找。这说明，初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成一个大的集合。

而在某次合并之后，有一种合理的需求：某两个元素是否已经处在同一个集合中了？因此就需要Find操作。

并查集的基本的数据表示：每个元素id的对应一个集合。

然后这种结构使用数组来存储，这样的话Find操作就是索引其中的某个位置的元素，事件复杂度是O(1)。

然后Union操作的话需要遍历整个数组一遍，事件复杂度是O(n)的，时间复杂度大，对于存储的元素数据量变得很大的时候，就比较鸡肋了。

然后这里可以使用树结构来作为并查集的数据存储结构，其实就是将每个元素看做是一个节点，然后是一个集合中的元素就存储在一个树中，然后拥有相同的根节点。具体的如下：

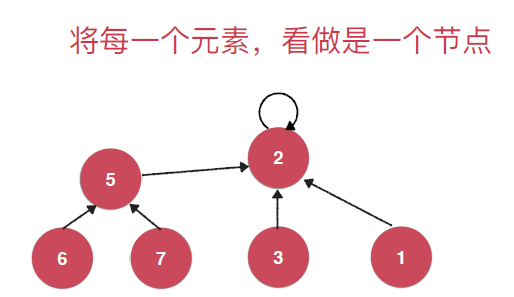
基于这种树结构实现的Find和Union操作的时间复杂度都是O(logn)的，综合来说好一些。

Quick Union

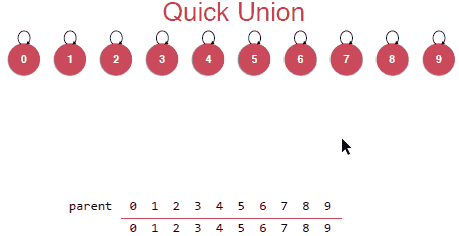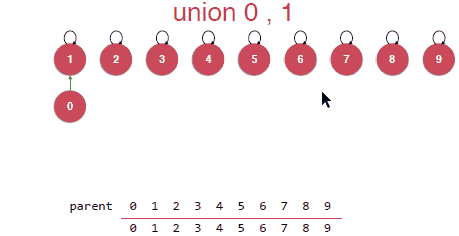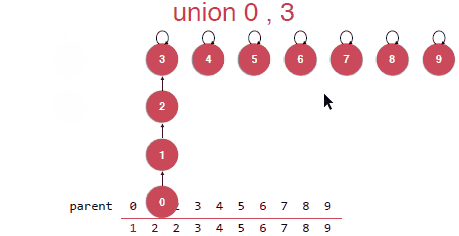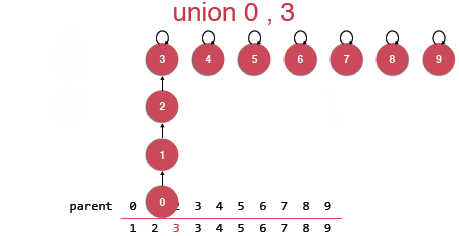
如何使用树结构来初始化并查集并且实现Quick Union操作，具体实现如下：

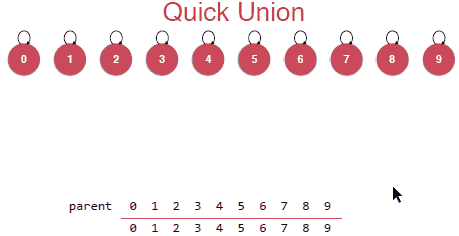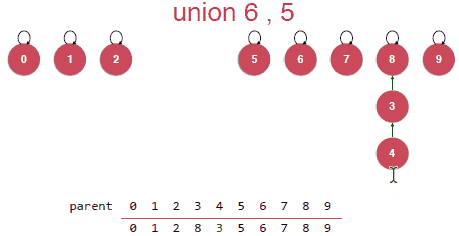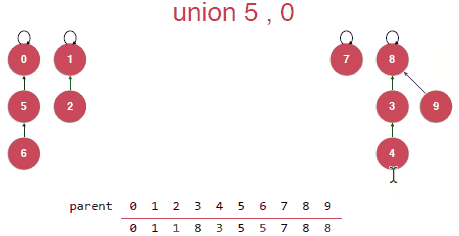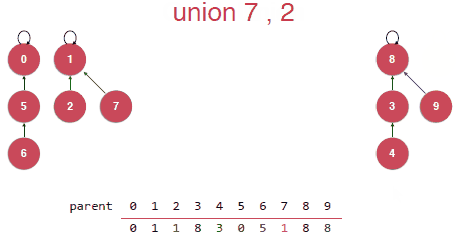
初始化的时候就是每个元素都是一棵树，并且根节点是指向自己的，表示每个元素是属于不同的集合的。

Union其实就是要将合并的元素指向其中某一个元素，由该元素作为根节点，指向同一个根节点的所有元素都是属于同一个集合的。

然后这样的Union操作其实是存在问题的，在合并的时候是可能将将树初始化成一个链表的如下如，这样的话树结构的优势就失去了。

我们并不希望出现这样的问题，那如何来完善呢？

基于size的union优化

我们可以新建一个空间来存储每棵树的size的大小，然后合并的时候讲size小的树合并到size大的树的根节点上，具体就如下图：

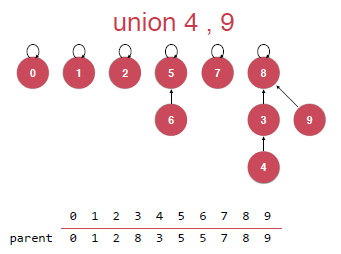
而不是这样去合并：

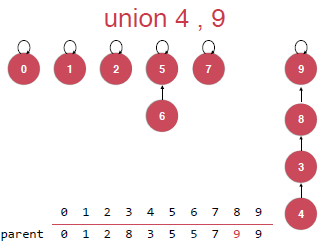
基于rank的union优化

上面这样的方式其实避免了合并的时候合并成了链表，但是还有一个问题，就是如下图的合并：

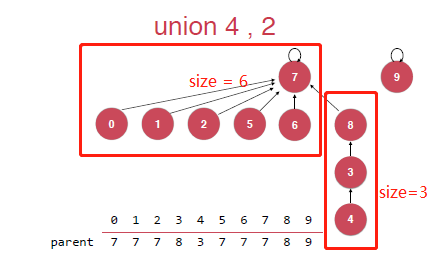
明显还是有问题的，我们希望的合并其实是将左边的树合并到右边的树上，而不是像上面这样，这样其实也是增加了树的深度，我们的union操作的时间复杂度是和树的深度有关系的。我们希望的合并方式是如下图的：

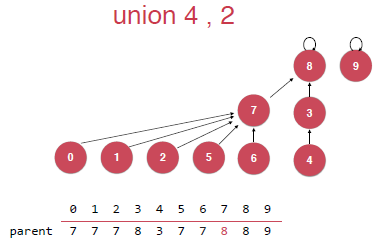
这就是基于rank的合并方式。

我们需要新建一个存储空间，用rank(i)表示已i为根节点的树的深度。

路径压缩

在find操作的时候，对于一个树，我们查找的时间复杂度其实也是和树的深度相关的，对于下面右边的树我们要find(4)也就是找4所在树（集合）的根节点，需要从末尾遍历到根部，但还是对于右边的话我们就不需要了，然后这两棵树是代表一样的集合。这就是路径压缩。

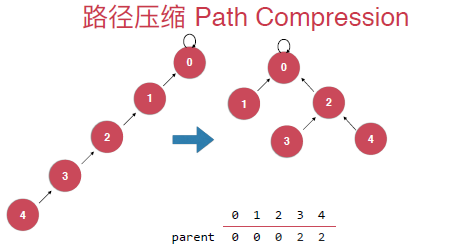
具体的实现其实就是将每次查找的元素的指向的节点指向其父亲节点的父亲节点。具体如下：

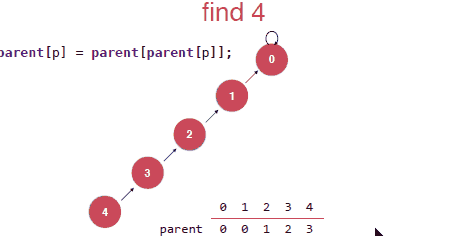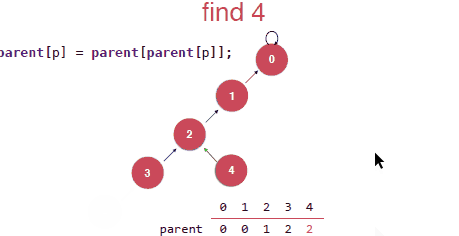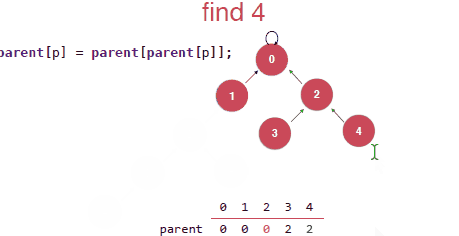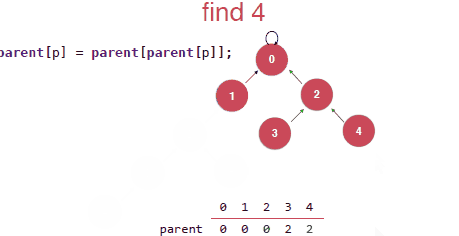
最后就是觉得上面压缩的还不是最优的，压缩成下面才是最优的，但是这种实现是需要递归的去实现，其实递归的过程本身也是需要付出代价的。所以这里讨论上面那种压缩的具体的实现。

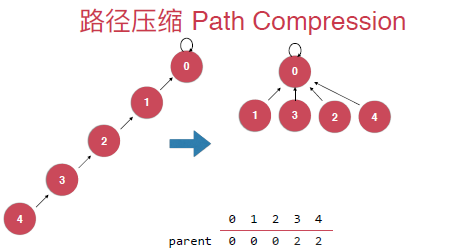
其实这两种路径压缩的实现具体的实现上的不同之处就在于：

private int find(int p){
        if (p < 0 || p > parent.length){
            throw  new IllegalArgumentException("p is illegal");
        }
        while (parent[p] != p){
            parent[p] = parent[parent[p]];
            p = parent[p];         //第一种压缩
//            parent[p] = find(parent[p]);  //第二种压缩
        }
        return parent[p];
    }

代码实现

package UnionFind;

/**
 * 基于树结构并查集
 * @author WilsonSong
 * @date 2018/6/15
 */
public class UnionFind implements UF {
    private int[] parent;

    private int[] rank;

    /**
     * 并查集的初始化
     * @param size
     */
    public UnionFind(int size){
        parent = new int[size];
        rank = new  int[size];
        for (int i = 0; i < size; i++){
            parent[i] = i;
            rank[i] = 1;
        }
    }

    /**
     * 找到p所在的集合
     * @param p 节点
     * @return
     */
    private int find(int p){
        if (p < 0 || p > parent.length){
            throw  new IllegalArgumentException("p is illegal");
        }
        while (parent[p] != p){
            parent[p] = parent[parent[p]];
            p = parent[p];
//            parent[p] = find(parent[p]);
        }
        return parent[p];
    }

    /**
     * 查看元素p和元素q是否所属一个集合
     * @param p
     * @param q
     * @return
     */
    @Override
    public boolean isConnected(int p, int q){
        return find(p) == find(q);
    }

    /**
     * 合并两个集合
     * @param p
     * @param q
     */
    @Override
    public void UnionElements(int p, int q){
        if (p < 0 || q < 0 ||  p > parent.length || q > parent.length){
            throw new IllegalArgumentException("index is illegal");
        }
        int pRoot = find(p);
        int qRoot = find(q);
        if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] = pRoot;
        }else if (rank[pRoot] < rank[qRoot]){
            parent[pRoot] = qRoot;
        }else {
            parent[pRoot] = pRoot;
            rank[pRoot] += 1;
        }
    }
}

时间复杂度

其实我上面所说的O(logn)的是不准确的，具体的如下：