AVL树的思想及实现
定义
AVL树是高度平衡的二叉搜索树,按照二叉搜索树(Binary Search Tree)的性质,AVL首先要满足:
若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树。
AVL树的性质:
- 左子树和右子树的高度之差的绝对值不超过1
- 树中的每个左子树和右子树都是AVL树
- 每个节点都有一个平衡因子(balance factor–bf),任一节点的平衡因子是-1,0,1之一,(每个节点的平衡因子bf 等于右子树的高度减去左子树的高度 )
下图就是一棵AVL Tree:
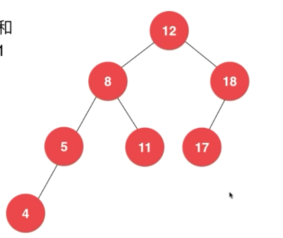
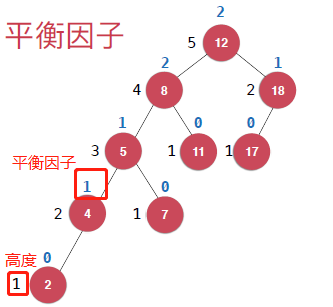
如下图,这棵树是非AVL树,因为其平衡因子是不满足要求的。
初始化AVL Tree
AVL树是高度平衡的二分搜索树,所以其初始化的时候和二分搜索树是一样的,只不过因为要计算平衡因子,所以需要记录每个节点的高度。
1 | public class AVLTree<K extends Comparable<K>, V> { |
计算高度和平衡因子
节点在初始化的时候的高度为1,然后树的初始化过程中会维护树的高度,所以获取节点的高度的话直接返回该节点的高度值就可以了。
平衡因子其实就是左子树的高度减去右子树的高度。
具体的实现如下:
1 | /** |
验证二分搜索树的性质和平衡性
AVL树是一颗高度平衡的二分搜索树,所以要满足二分搜索树的性质,也要满足平衡性。
验证是否是二分搜索树的话,二分搜索树的中序遍历之后的元素是满足顺序从大到小的顺序性的,所以可以用该性质来测试是否是二分搜索树。
平衡性就是判断平衡因子的绝对值是否大于0就可以了。
具体如下:
1 | /** |
维护平衡
有的时候给树中添加或者删除元素的时候可能会破坏树的平衡,那怎么去维护书的平衡呢?
右旋转
当插入的元素位于不平衡节点的左侧的左侧的时候:
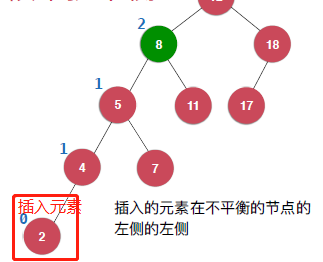
这个时候需要对8这个节点进行右旋转。
右旋转的具体的实现完成如下:
其实过程很简单就是将y的做节点换成x的有节点,然后x的右孩子指向y.
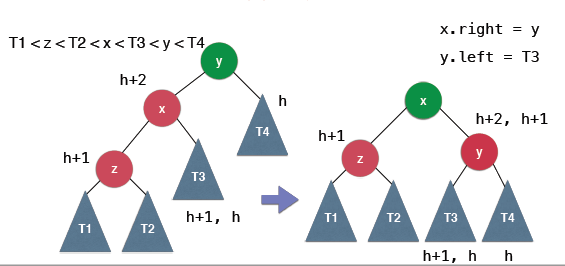
具体的过程如下:
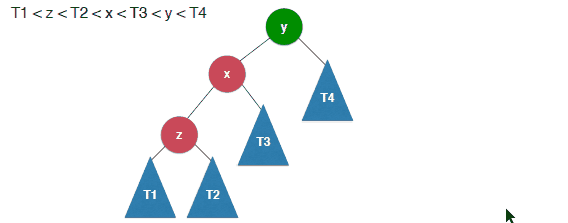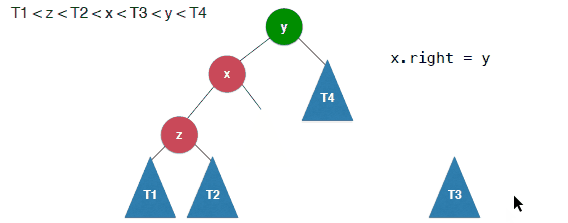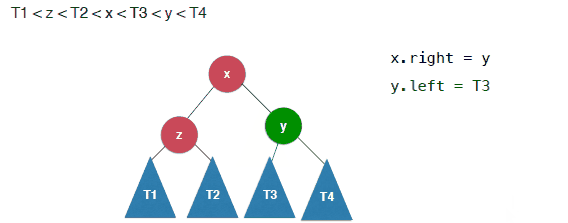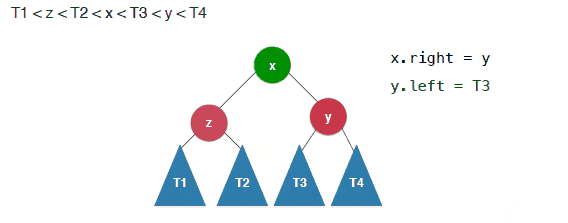
1 | /** |
左旋转
当插入的元素位于不平衡节点的右侧的右侧的时候,需要进行左旋转,其实和右旋转是一个对称的过程,不在赘述,具体如下:
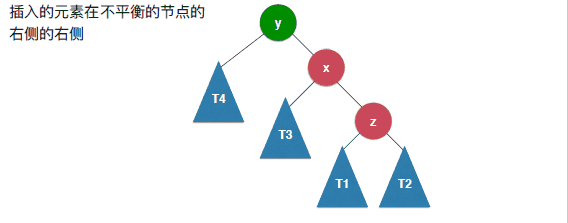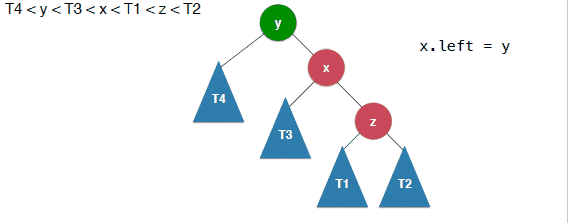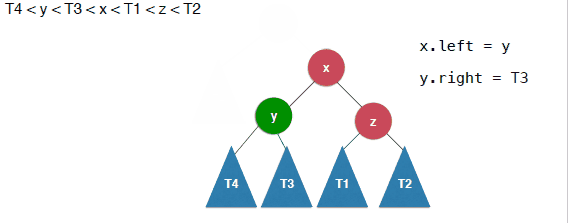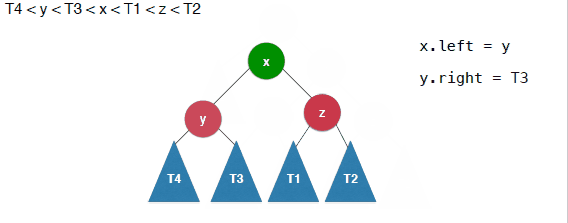
1 | /** |
先左旋转后右旋转
当插入的元素位于不平衡元素的左侧的右侧的时候需要先左旋转然后进行右旋转,为什么是这样的?
如下图的情况:
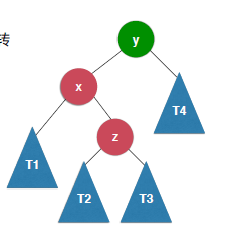
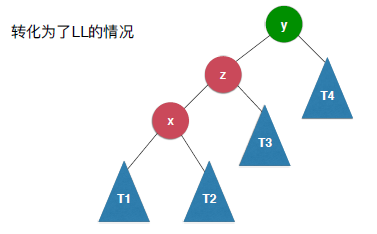
对X进行了左旋转之后变成了上面介绍的需要进行右旋转的情况,这时候只需要在进行右旋转就可以维持平衡了。
先右旋转后左旋转
当插入的元素位于不平衡元素的右侧的左侧的时候需要先左旋转然后进行右旋转,为什么是这样的?
如下图的情况:
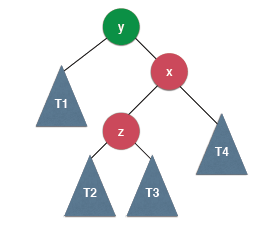
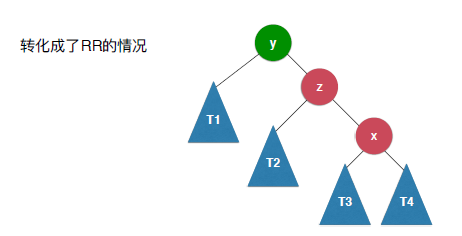
对X进行了右旋转之后变成了上面介绍的需要进行左旋转的情况,这时候只需要在进行左旋转就可以维持平衡了。
插入元素
其实插入元素的过程是和二分搜索树是一样的,只不过AVL树多了一些操作,插入元素之后需要更新节点的高度,需要判断是否平衡,不平衡的话属于那种不平衡的情况需要进行什么操作来维护平衡?其实就是逻辑上的判断。
具体的实现如下
1 | /** |
删除元素
其实删除元素的过程是和二分搜索树是一样的,删除叶子节点的话直接删除皆可以了,然后删除节点话需要找到该叶子节点的右子树中的最小值来重新成为该树的根节点,还有AVL树还多了一些操作,删除元素之后需要更新节点的高度,需要判断是否平衡,不平衡的话属于那种不平衡的情况需要进行什么操作来维护平衡?其实也还是逻辑上的判断。
具体实现如下:
1 | /** |
完整代码
1 | package AVLTree; |
