Fork me on GitHub

红黑树思想详解及实现

发表于 | 分类于 |
本文共计: 3,578 | 阅读耗时 ≈ 14

红黑树思想详解及实现

从2-3树开始

2-3树定义

2-3树在《算法4》这本树中的定义是这样子的：

一棵2-3查找树或为一棵空树，或由以下节点组成：

  1. 2-节点，含有一个键（及其对应的值）和两条链接，左链接指向的2-3树中的键都小于该节点，右链接指向的2-3树中的节点值都大于该节点。
  2. 3-节点，含有两个键（及其对应的值）和三条链接，左链接指向的2-3树中的键都小于该节点，中连接指向的2-3树中的键值位于两个键值之间，右链接指向的2-3树的节点都大于该节点。

其实2-3树是一个绝对平衡的二分查找树，什么叫绝对平衡？就是叶子节点的高度是相同的，或者说任一节点到空节点的距离是相同的。

下图就是一棵2-3树：

1

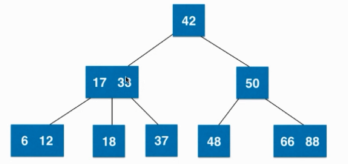
2-3树如何维持绝对平衡

2-3树维持平衡的过程其实就是当来一个一个节点的时候先与其要存储的位置的父亲节点进行融合，组成一个2节点，然后在来一个元素的话继续融合，然后这个时候其实这个节点是一个4节点，我们的2-3树中是没有4节点的，这个时候就将这个4节点退化成3个2节点。每次添加元素的时候都是这样的操作，当一个子节点添加成为4节点然后退化的时候成3个两节点的时候就需要将该根节点并到其父亲节点上。这样就可以保持树的平衡。

具体的的实现如下动画所示：

2

红黑树与2-3 树的等价性

红黑树顾名思义红色和黑色的树，其实就是树中存在红色的节点和黑色的节点。那红色的节点和黑色的节点给带变什么意思呢？

其实一个黑色的节点表示2-3树中的2-节点，一个黑色的节点加上其左孩子为红色的节点这两个节点表示3-节点。其实也就是黑色节点和作为其左孩子的红色节点是在树上的一层的。

3

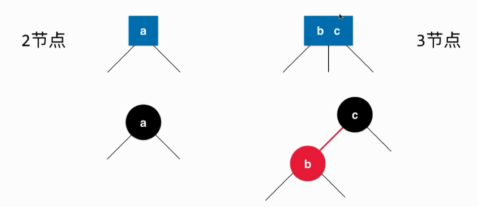
然后看一个2-3树与红黑树等价的例子：

4

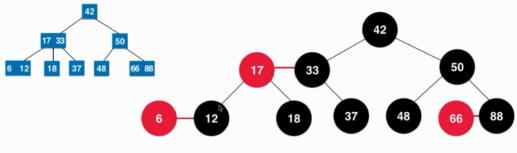
红黑树的性质

  1. 每个节点或者是红色的，或者是黑色的

  2. 根节点是黑色的

  3. 每一个叶子节点（最后的空节点）是黑色的
  4. 如果一个节点是红色的，其孩子节点都是黑色的
  5. 从任意一个节点到叶子节点经过的黑色的节点的数量是相同的

怎么理解这些性质呢？

首先每个节点是红色或者黑色，红黑树中就这两种颜色的节点，没啥可说的。

然后是根节点是黑色的，为什么说根节点是黑色的呢？可以从2-3树的角度来理解，比方说2-3树的根节点是2-节点的，肯定是黑色的，然后手机3节点的也会退化成一个黑色节点带一个红色左孩子的节点，就算是空树，我们知道最后的空节点也是黑色的。这就与第3条性质吻合。

然后是叶子节点都是黑色的，也就是最后的空节点都是黑色的，其实他就是定义空的是黑色的。

接着是一个红色节点的两个孩子节点都是黑色的，首先反推一下，你想两个红色节连在一起，然后其父亲节点一定是有个黑色节点，那这样就对应成了2-3树中的4节点，明显是不成立的。然后正向看一下，对应2-3树中，一个红色节点肯定是一个3节点，其孩子节点要么是一个2节点要么是一个3节点，2节点的话肯定是黑色的，3节点的话也会是一个黑色节点带一个红色的左孩子节点，那链接在黑色节点上的肯定也是黑色的节点。

最后一条性质，从任意一个节点到叶子节点经过的黑色的节点的数量是相同的，红黑树是一颗绝对黑平衡的树，其实即使黑色节点构成的树是绝对平衡的，然后也可以从2-3树的角度理解，2-3树是一颗绝对平衡的树，不管2节点还是3-节点，其一定是由一个黑色节点的，所以黑色节点树就是绝对平衡的。所以从任意一个节点到叶子节点经过的黑色的节点的数量是相同的。

通过以上的定义我们就可以初始化一棵红黑树了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class RedBlackTree<K extends Comparable<K>, V> {

    private static final boolean BLACK = false;
    private static final boolean RED = true;
    /**
     * 树节点的底层实现
     */
    private class Node{
        public K key;
        public V value;
        public boolean color;

        public Node leftNode;
        public Node rightnode;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            color = RED;     //从红黑树的定义来看，每个节点初始化都是红色节点
            leftNode = null;
            rightnode = null;
        }
    }

    private Node root;
    private int size;

    /**
     * 构造函数
     */
    public RedBlackTree(){
        root = null;
        size = 0;
    }

向红黑树中添加元素

首先我们从2-3是树开始去理解添加元素的操作，要是向2-节点添加元素的话就是直接添加形成一个3-节点，要是向3-节点添加元素的话就是先形成4节点，然后退化成3个两节点，而且添加的话都是添加的红色的节点，然后通过一些列的变换可以让其变成符合要求的红黑树。

那向红黑树中添加元素需要考虑哪些问题呢？

首先某一棵树中的根节点是黑色的，然后来一个元素，比他小，按照二分搜索树的规则，我们把它插入到根节点的左侧，并且是红色的节点，其实现在就相当于2-3树中的3-节点。正好满足要求不需要任何处理，直接添加即可。

当要插入的元素是大于黑色节点的话，需要将这个红色的节点插入到黑色节点的右侧，这时候是不满足红黑树的原则的，需要进行左旋转来让其满足红黑树的要求。

左旋转

左旋转的具体过程如下：

5

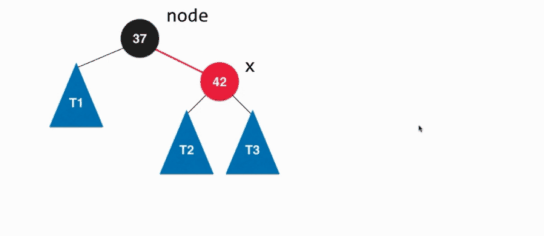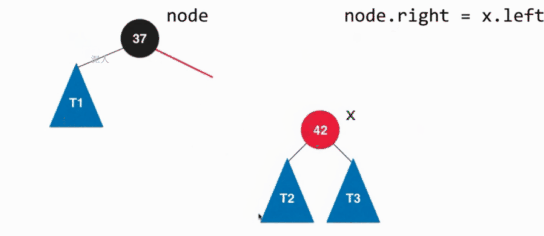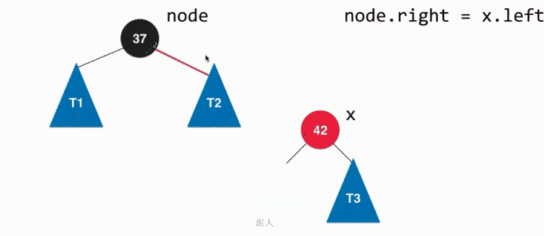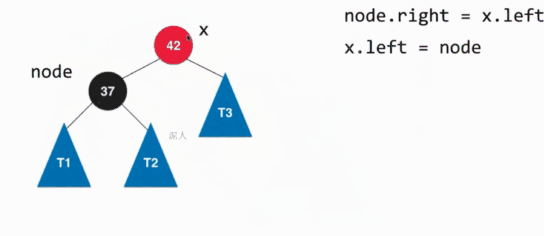
其实就是将根节点作为原来孩子的左孩子节点。通过左旋转之后就可以使红黑树满足要求，但是还是需要对节点的颜色进行改变，因为当前的节点旋转之后节点的位置发生了改变，具体的就是让x节点的颜色变为原来节点的颜色，因为现在x是根节点了，原来根节点是什么颜色，现在x就是什么颜色。然后让原来的节点颜色变为红色，因为旋转之后还是3节点，为了保持其实3节点，所以就将原来的节点颜色变为红色。

具体代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
     * 为了保持红黑树性质进行左旋转
     //   node                     x
     //  /   \     左旋转         /  \
     // T1   x   --------->   node   T3
     //     / \              /   \
     //    T2 T3            T1   T2
     * @param node node
     * @return
     */
    private Node leftRotate(Node node){
        Node x = node.rightnode;
        node.rightnode = x.leftNode;
        x.leftNode = node;

        //变更节点的颜色，现在的根节点的颜色要与原来根节点颜色相同，
        //原来的根节点现在变成孩子节点，颜色是红色
        x.color = node.color;
        node.color = RED;
        return x;
    }

颜色反转

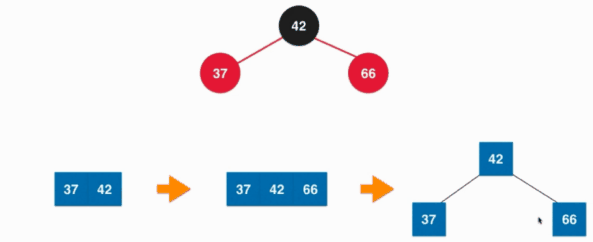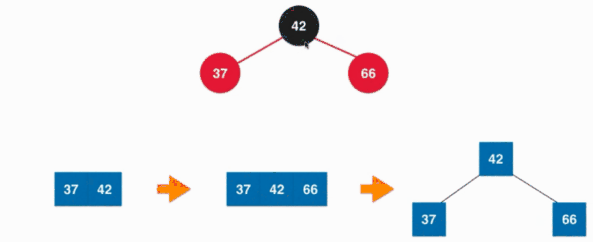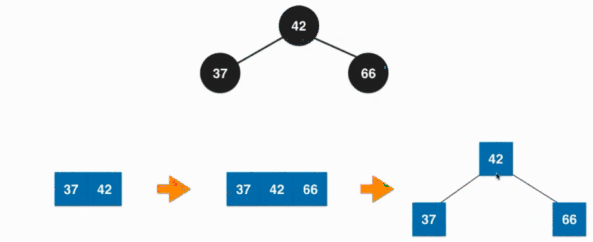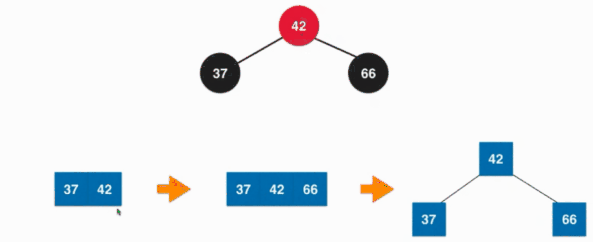
插入元素的时候并不只会发生上面一种情况使其不满足红黑树的要求，例如向3节点中插入元素的时候，插入元素之后形成了具体就像下面这种情况：

6

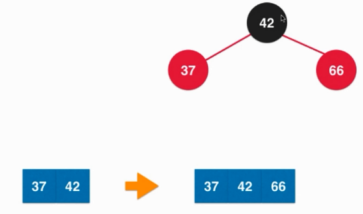
那怎么去处理这样的情况呢？其实按照定义，这个4节点会退化成3个两节点，也就是让所有的树的节点的颜色变为黑色就可以了，但是3个两节点之后根节点我们还会向上去合并，所有将根节点变为红色。其实也就是我们将树节点的颜色反转一下就可以让其满足了红黑树的要求：

具体如下：

7

代码实现：

1
2
3
4
5
6
7
8
9
/**
     * 颜色反转
     * @param node node
     */
    private void flipColors(Node node){
        node.leftNode.color = BLACK;
        node.rightnode.color = BLACK;
        node.color = RED;
    }

右旋转

还有一种添加元素导致的情况如下图：

8

其实也就是新添加的元素是添加在红色节点的左孩子上，这个时候就不满足红黑树中红色节点的左右孩子都是黑色的性质了，这个时候就需要右旋转处理。具体如下：

9

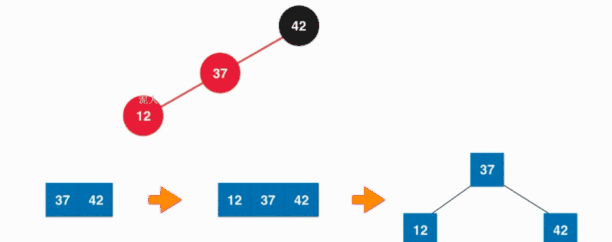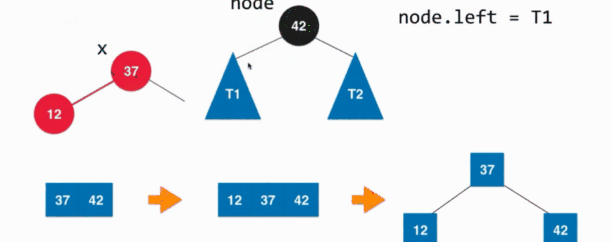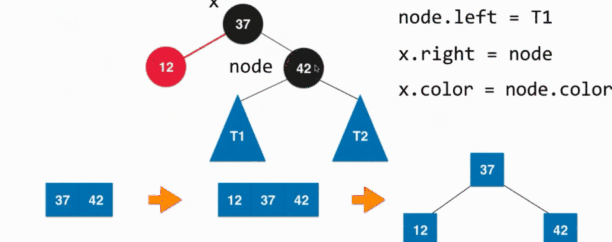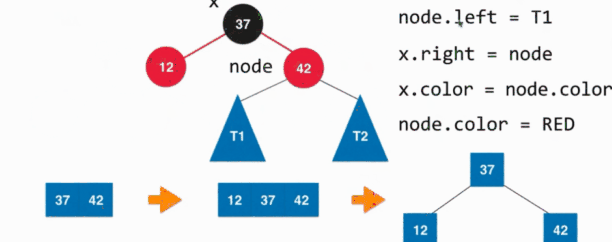
其实我们看右旋转完成之后，以为节点的颜色发生变化，还是和左旋转一样的方法去改变旋转后改变的节点的颜色。然后改变完成之后我们发现其是这时候树的样式是和颜色反转时候的情况是一样的，所以这时候进行一下颜色的反转就可以了。

具体的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
     * 为了保持红黑树性质进行右旋转
     //     node                   x
     //    /   \     右旋转       /  \
     //   x    T2   ------->   y   node
     //  / \                       /  \
     // y  T1                     T1  T2
     * @param node node
     * @return
     */
    private Node rightRotate(Node node){

        Node x = node.leftNode;
        // 右旋转
        node.leftNode = x.rightnode;
        x.rightnode = node;

        x.color = node.color;
        node.color = RED;
        return x;
    }

整合流程

其实在添加元素的时候还有一种情况是需要考虑的，就是添加的元素添加的位置是红色节点的右孩子，这显然也是不满足红黑树的性质的。

10

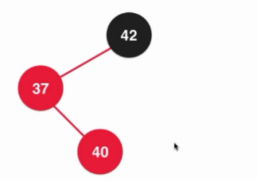
这种情况怎么去处理呢？其实可以先37节点左旋转——>然后42右旋转—->调整节点颜色——>颜色反转其实完成了整个的操作，是添加进新的元素后的树也是满足红黑树的性质的。

具体的过程如下：

11

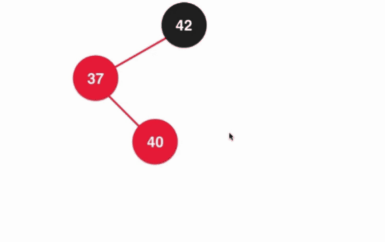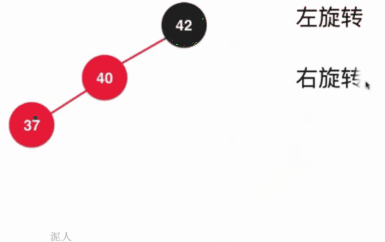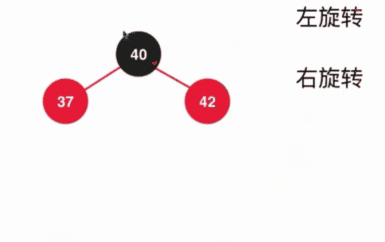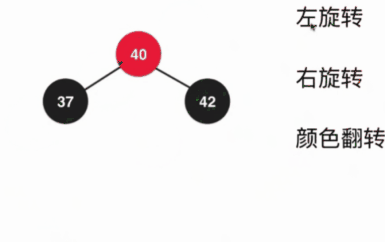
其实这个过程是组合了上面讨论的所有情况，所以既然这中情况是所有的问题都会考虑到的话，那其实就可以添加元素的时候组合成下面的过程：

12

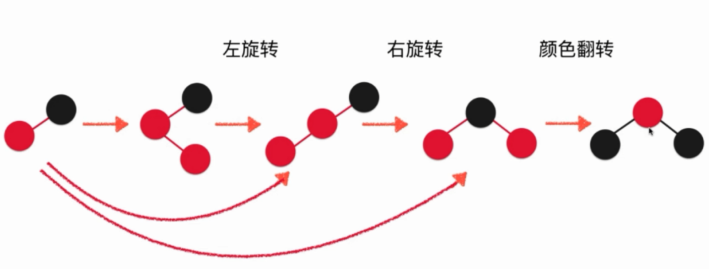
也就是每次添加元素的时候只需要判断出现了那种情况，然后依次跳转到其需要进行的操作上去就可以了，不需要每个都进行重复的流程操作。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
package RedBlackTree;

/**
 * 红黑树的底层简单实现
 * @author WilsonSong
 * @date 2018/6/26
 */
public class RedBlackTree<K extends Comparable<K>, V> {

    private static final boolean BLACK = false;
    private static final boolean RED = true;
    /**
     * 树节点的底层实现
     */
    private class Node{
        public K key;
        public V value;
        public boolean color;

        public Node leftNode;
        public Node rightnode;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            color = RED;     //从红黑树的定义来看，每个节点初始化都是红色节点
            leftNode = null;
            rightnode = null;
        }
    }

    private Node root;
    private int size;

    /**
     * 构造函数
     */
    public RedBlackTree(){
        root = null;
        size = 0;
    }

    /**
     * 获取某个key对应的node
     * @param node node
     * @param key key
     * @return Node node
     */
    public Node getNode(Node node,K key){
        if (node == null){
            return null;
        }

        if (node.key.equals(key)){
            return node;
        }else if (node.key.compareTo(key) > 0){
            return getNode(node.leftNode, key);
        }else {
            return getNode(node.rightnode, key);
        }
    }

    /**
     * 判断节点是否为红色
     * @param node node
     * @return
     */
    public boolean isRed(Node node){
        if (node == null){
            return BLACK;
        }
        return node.color;
    }


    /**
     * 为了保持红黑树性质进行左旋转
     //   node                     x
     //  /   \     左旋转         /  \
     // T1   x   --------->   node   T3
     //     / \              /   \
     //    T2 T3            T1   T2
     * @param node node
     * @return
     */
    private Node leftRotate(Node node){
        Node x = node.rightnode;
        node.rightnode = x.leftNode;
        x.leftNode = node;

        //变更节点的颜色，现在的根节点的颜色要与原来根节点颜色相同，
        //原来的根节点现在变成孩子节点，颜色是红色
        x.color = node.color;
        node.color = RED;
        return x;
    }

    /**
     * 为了保持红黑树性质进行右旋转
     //     node                   x
     //    /   \     右旋转       /  \
     //   x    T2   ------->   y   node
     //  / \                       /  \
     // y  T1                     T1  T2
     * @param node node
     * @return
     */
    private Node rightRotate(Node node){

        Node x = node.leftNode;
        // 右旋转
        node.leftNode = x.rightnode;
        x.rightnode = node;

        x.color = node.color;
        node.color = RED;
        return x;
    }

    /**
     * 颜色反转
     * @param node node
     */
    private void flipColors(Node node){
        node.leftNode.color = BLACK;
        node.rightnode.color = BLACK;
        node.color = RED;
    }

    /**
     * 添加元素
     * @param key key
     * @param value value
     */
    public void add(K key, V value){
        root = add(root, key, value);
        root.color = BLACK;             //根节点的颜色一定是黑色的
    }

    /**
     * 递归的向以node为根节点的树中添加元素
     * @param node node
     * @param key key
     * @param value value
     * @return 返回添加元素后的子树的根
     */
    private Node add(Node node, K key, V value){
        if (node == null){
            node = new Node(key, value);
            size ++;
            return node;
        }

        if (node.key.compareTo(key) > 0){
            node =  add(node.leftNode, key, value);
        }else if (node.key.compareTo(key) < 0){
            node =  add(node.rightnode, key, value);
        }else {
            node.value =value;
        }

        //下面的每一步都要进行判断的，其实就是一个连接整合的过程
        //右子树红色，左子树是黑色
        if (isRed(node.rightnode) && !isRed(node.leftNode))
            node = leftRotate(node);

        //左子树为红色，左子树的左子树也为红色，右旋转
        if (isRed(node.leftNode) && isRed(node.leftNode.leftNode))
            node = rightRotate(node);

        //左右子树均为红色，只要颜色反转即可
        if (isRed(node.leftNode) && isRed(node.rightnode))
            flipColors(node);

        return node;
    }
}

本文标题:红黑树思想详解及实现

文章作者:WilsonSong

发布时间:2018年06月27日 - 10:06

最后更新:2018年08月31日 - 20:08

原始链接:https://songwell1024.github.io/2018/06/27/RedBlackTree/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------本文结束感谢您的阅读-------------