Fork me on GitHub

哈希表设计思想及实现

发表于 | 分类于 |
本文共计: 2,662 | 阅读耗时 ≈ 11

哈希表设计思想及实现

定义

哈希表在《算法4》这本书中是这么介绍的：哈希表其实又叫散列表，是算法在时间和空间上做出权衡的经典例子。如果一个表所有的键都是小整数，我们就可以用一个数组来实现无序的符号表，将键作为数组的索引而数组中i出存储的值就是它对应的值。其实散列表的思想也是这样的，只不过他的键的类型更加复杂，是这种简易方法的一种扩展。

使用散列查找分为两步：

  1. 用散列函数将被查找的键转换为数组的一个索引。理想情况下，不同的键值都会转换成为不同的索引值，但是一般情况下我们会遇到多个键对应相同的索引值，这也就是所谓的散列冲突。
  2. 处理碰撞冲突的情况，常用得方法有两种：拉链法（链地址法）和线性探测法，下面也会介绍这两种方法。

哈希函数

其实要设计一个哈希表首先要做的就是散列函数的计算，通过散列函数就可以将键转换为数组的索引。其实哈希函数的设计是一个非常常见的一个研究方向，就像在我们的网络安全的密码设计的过程中，散列函数就是一个非常重要的理论。但是这里介绍的是最一般的哈希函数的设计思想。

哈希函数其实就是将键准换为索引，那么这里的键可以用什么数据类型呢？其实常见的基本数据类型都可以，甚至是我们自己定义的数据类型也是可以的。下面将分开展开介绍。

正整数

对于小正整数的话直接用就可以了，对于小负整数的话进行一定的偏移就可以了，例如-100 - 100 —> 0 - 200

对于大整数散列最常用的方法是除留余数法。

例如一个身份证号：332112200007076666这个的话取模，让他模10000，取后4位6666作为索引，这样带来好处是节省空间，因为我们显然不可能开辟那么大的空间去让身份证号称为索引，太浪费空间了。但是这样也带来了一定的问题就是碰撞冲突的问题。还有一个问题就是直接取模的话容易造成键值的分布不均匀。所以一般采用的方式是模一个大素数，为什么是模一个素数就可以避免不均匀的情况，这个其实是数论里的问题，不探讨，知道方法就可以了。

关于上面的情况举个例子介绍下：

1
2
3
4
5
10 % 4 = 2         10 % 7 = 3
20 % 4 = 0         20 % 7 = 6
30 % 4 = 2         30 % 7 = 2
40 % 4 = 0         40 % 7 = 5
50 % 4 = 2         50 % 7 = 1

那素数怎么取呢？给出一般的参考的取值

1

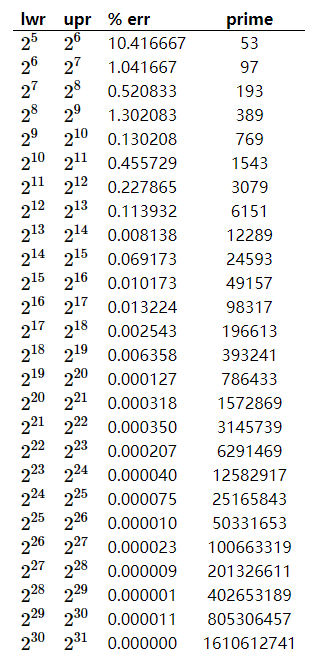
浮点数

浮点数的话其实也是转换成为整数，然后使用除留余数法。

那浮点数怎么转换成为整数呢？我们知道浮点数其实在计算机中是二进制数存在的，将二进制数变为整数就可以了。

2

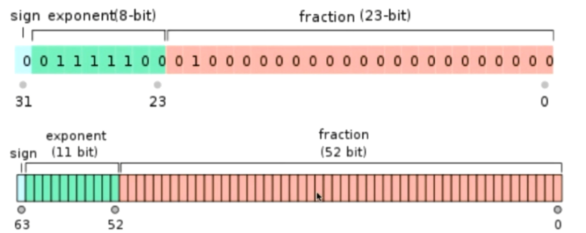
字符串

其实字符串我们也可以将其看成是大整数来处理。

举个例子：
$$
166 = 1 10^2 + 6 10^1+ 6*10^0
$$

$$
code = cB^3+oB^2+dB^1+eB^0
$$

$$
hash(code) =(cB^3+oB^2+dB^1+eB^0)\%M
$$

$$
hash(code) =((((cB)+o)B+d)*B+e))\%M
$$

$$
hash(code) =((((c\%M)B+o)\%MB+d)\%M*B+e))\%M
$$

其实左后就准换成为上面公式的样子，其中B表示进制，M表示模的素数。

其实转换成代码就是下面这样的：

1
2
3
int hash = 0;
for(int i = 0; i < s.length(); i++ )
    hash = (hash * B + s.charAt(i))%M

组合类型

所谓的组合类型也就是自定义的数据类型，也是可以转换成为大整数来处理。

例如我定义了一个Student的数据类型

Student：name , number,score:

计算student的散列值如下：
$$
hash(student) = (((student.name\%M)B + student.number)\%MB + student.socre)\%M
$$

链地址法（拉链法）

链地址法的原理时如果遇到冲突，他就会在原地址新建一个空间，然后以链表结点的形式插入到该空间。下面从百度上截取来一张图片，可以很清晰明了反应下面的结构。比如说我有一堆数据{1,12,26,337,353…}，而我的哈希算法是H(key)=key mod 16，第一个数据1的哈希值f(1)=1，插入到1结点的后面，第二个数据12的哈希值f(12)=12，插入到12结点，第三个数据26的哈希值f(26)=10，插入到10结点后面，第4个数据337，计算得到哈希值是1，遇到冲突，但是依然只需要找到该1结点的最后链结点插入即可，同理353。

　　3

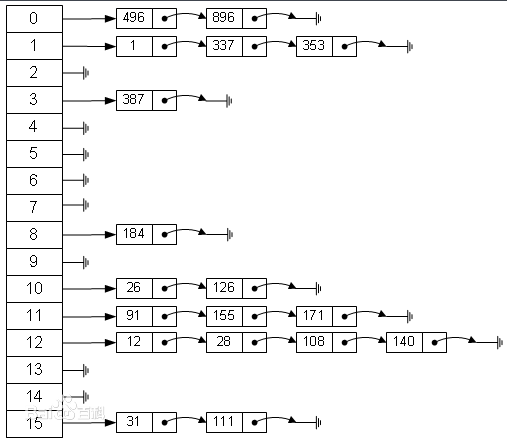
把一个值得hash值转换为一个数组的索引的代码如下：

1
2
3
private int hash(K key){
    return (key.hashCode() & 0x7ffffff)%M;
}

通过& 0x7ffffff这种方式就可以将符号位屏蔽，也就是说我们就算是传入负数也没有关系。

上面的图是每个地址存的是一个链表，在java8中当冲突达到一定的数量的时候就会将链表转换为红黑树，我们下面的实现用地址存一个TreeMap（java中的TreeMap的底层其实就是用红黑树来实现的）来具体的实现。

5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
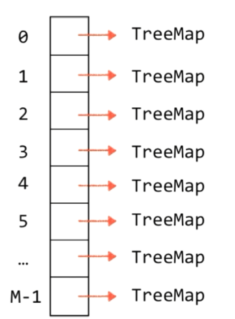
import java.util.TreeMap;

public class HashTable<K, V> {

    private TreeMap<K, V>[] hashtable;
    private int size;
    private int M;

    public HashTable(int M){
        this.M = M;
        size = 0;
        hashtable = new TreeMap[M];
        for(int i = 0 ; i < M ; i ++)
            hashtable[i] = new TreeMap<>();
    }

    public HashTable(){
        this(97);
    }

    private int hash(K key){
        return (key.hashCode() & 0x7fffffff) % M;
    }

    public int getSize(){
        return size;
    }

    public void add(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if(map.containsKey(key))
            map.put(key, value);
        else{
            map.put(key, value);
            size ++;
        }
    }

    public V remove(K key){
        V ret = null;
        TreeMap<K, V> map = hashtable[hash(key)];
        if(map.containsKey(key)){
            ret = map.remove(key);
            size --;
        }
        return ret;
    }

    public void set(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if(!map.containsKey(key))
            throw new IllegalArgumentException(key + " doesn't exist!");

        map.put(key, value);
    }

    public boolean contains(K key){
        return hashtable[hash(key)].containsKey(key);
    }

    public V get(K key){
        return hashtable[hash(key)].get(key);
    }
}

动态空间处理

我们上实现的时候把M的值取成了固定值，这个时候我们来分析下他的时间复杂度：

如果放入哈希表中的元素的个数使N，每个地址中存放的元素的个数是N/M的，然后每个地址中存放的是TreeMap，也就是底层是红黑树，对于一个红黑树的查询一个元素的时间复杂度是O(logN/M)的。然而对于哈希表其实是查询的复杂度应该是O(1)的复杂度，因为底层就是数组，直接索引一个数组中的值也就是O(1)的复杂度。

但是这里明显不符合啊？其实就是开辟的空间是固定的导致的，我们需要进行动态空间处理。怎么处理呢？其实就是把和动态数组的处理是一样的。当元素的个数大于阈值的时候就扩大空间，小于阈值时就压缩空间，具体如下：

当平均每个地址承载的元素多过一定程度时就扩容：n/M >= upperTol;

当平均每个地址承载的元素少于一定程度时就缩容：n/M < lowerTol;

扩容的时候怎么去扩大，扩大成多少呢？因为空间的大小其实也就是我们要模的那个值，所以选取扩大空间大小是有要求的。其实扩大的参考值就是上面给出素数取值时一般参考的取值。

具体的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private void resize(int newM){
        TreeMap<K, V>[] newHashTable = new TreeMap[newM];
        for(int i = 0 ; i < newM ; i ++)
            newHashTable[i] = new TreeMap<>();

        int oldM = M;
        this.M = newM;
        for(int i = 0 ; i < oldM ; i ++){
            TreeMap<K, V> map = hashtable[i];
            for(K key: map.keySet())
                newHashTable[hash(key)].put(key, map.get(key));
        }

        this.hashtable = newHashTable;
    }

开放地址法

实现哈希表的另一种方式就是用大小为M的数组保存N个键值对，其中M > N。我们需要依靠数组中的空位解决碰撞冲突。基于这种策略的所有方法给统称为开放地址散列表。

其实就是使用开放地址法来解决碰撞冲突的问题。具体的开放地址法是怎么来解决碰撞冲突的，书上给出的解释是这样的：

6

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
import java.util.TreeMap;

public class HashTable<K extends Comparable<K>, V> {

    private final int[] capacity
            = {53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
            49157, 98317, 196613, 393241, 786433, 1572869, 3145739, 6291469,
            12582917, 25165843, 50331653, 100663319, 201326611, 402653189, 805306457, 1610612741};

    private static final int upperTol = 10;
    private static final int lowerTol = 2;
    private int capacityIndex = 0;

    private TreeMap<K, V>[] hashtable;
    private int size;
    private int M;

    public HashTable(){
        this.M = capacity[capacityIndex];
        size = 0;
        hashtable = new TreeMap[M];
        for(int i = 0 ; i < M ; i ++)
            hashtable[i] = new TreeMap<>();
    }

    private int hash(K key){
        return (key.hashCode() & 0x7fffffff) % M;
    }

    public int getSize(){
        return size;
    }

    public void add(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if(map.containsKey(key))
            map.put(key, value);
        else{
            map.put(key, value);
            size ++;

            if(size >= upperTol * M && capacityIndex + 1 < capacity.length){
                capacityIndex ++;
                resize(capacity[capacityIndex]);
            }
        }
    }

    public V remove(K key){
        V ret = null;
        TreeMap<K, V> map = hashtable[hash(key)];
        if(map.containsKey(key)){
            ret = map.remove(key);
            size --;

            if(size < lowerTol * M && capacityIndex - 1 >= 0){
                capacityIndex --;
                resize(capacity[capacityIndex]);
            }
        }
        return ret;
    }

    public void set(K key, V value){
        TreeMap<K, V> map = hashtable[hash(key)];
        if(!map.containsKey(key))
            throw new IllegalArgumentException(key + " doesn't exist!");

        map.put(key, value);
    }

    public boolean contains(K key){
        return hashtable[hash(key)].containsKey(key);
    }

    public V get(K key){
        return hashtable[hash(key)].get(key);
    }

    private void resize(int newM){
        TreeMap<K, V>[] newHashTable = new TreeMap[newM];
        for(int i = 0 ; i < newM ; i ++)
            newHashTable[i] = new TreeMap<>();

        int oldM = M;
        this.M = newM;
        for(int i = 0 ; i < oldM ; i ++){
            TreeMap<K, V> map = hashtable[i];
            for(K key: map.keySet())
                newHashTable[hash(key)].put(key, map.get(key));
        }

        this.hashtable = newHashTable;
    }
}

本文标题:哈希表设计思想及实现

文章作者:WilsonSong

发布时间:2018年07月01日 - 16:07

最后更新:2018年09月02日 - 10:09

原始链接:https://songwell1024.github.io/2018/07/01/HashTable/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

-------------本文结束感谢您的阅读-------------